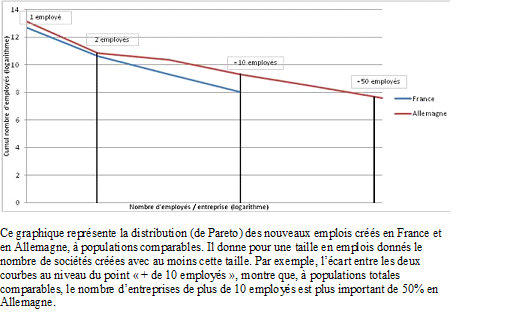
Comme l’a montré Benoît Mandelbrot, la loi de Pareto est assez universelle et commande beaucoup de distributions associées à la taille des entreprises. Elle permet, à partir d’une distribution discrète de tailles, de reconstituer complètement la population.
La loi de Pareto dont la première forme s’écrit Log N(x)= Log A –? Log x où N(x) représente les effectifs de revenu supérieur à x, a été associée, dès son énoncé dans le Cours d’Économie Politique par Pareto puis par un grand nombre d’économistes statisticiens, à un débat très houleux sur la mesure des inégalités de revenus ou de fortunes .
Benoît Mandelbrot, dans un certain nombre d’ouvrages célèbres (Les objets fractals, 1975, The fractal geometry of nature, 1982) a montré que la loi de Pareto s’étendait à une énorme série d’objets ou de séries : la dimension des galaxies, des villes, la taille des sauts des valeurs de bourse ou des crues du fleuve Nil, etc..
Elle se retrouve dans la distribution de la taille des entreprises que ce soit en capitaux propres, capital social ou effectifs.
Elle peut être distinguée de la loi de Gibrat ou loi Log normale où c’est le logarithme de la variable qui suit une loi normale.
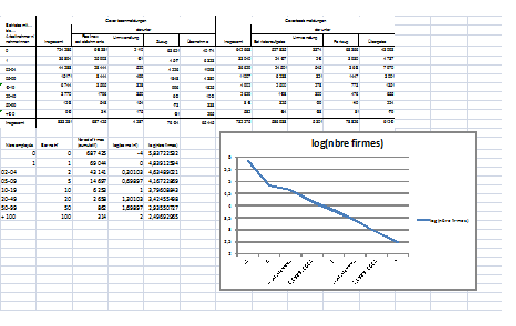
Une propriété intéressante est que sauf pour des valeurs entières du coefficient ?, les intégrales et les dérivées de la loi de Pareto restent des lois de Pareto.
Cette loi est extrêmement commode pour « combler les trous » dans les informations économiques données de façon discrètes, comme des nombres d’objet par classe ce qui est souvent le cas.
On part alors de la classe n qui contient le plus petit nombre d’objet Yn au-delà de la valeur Xn et on lui ajoute le nombre d’objets Yn-1 et ainsi de suite. Log (Yn+Yn-1+ …+Yn-p) est une fonction linéaire de Xn-p.
On a donné ci-dessous un exemple de courbe de Pareto tracée à partir des statistiques de Destatis (un INSEE allemand) sur les créations d’entreprises en Allemagne (éliminant les entreprises qui ne sont pas de réelles créations comme des reprises ou des changements de noms).
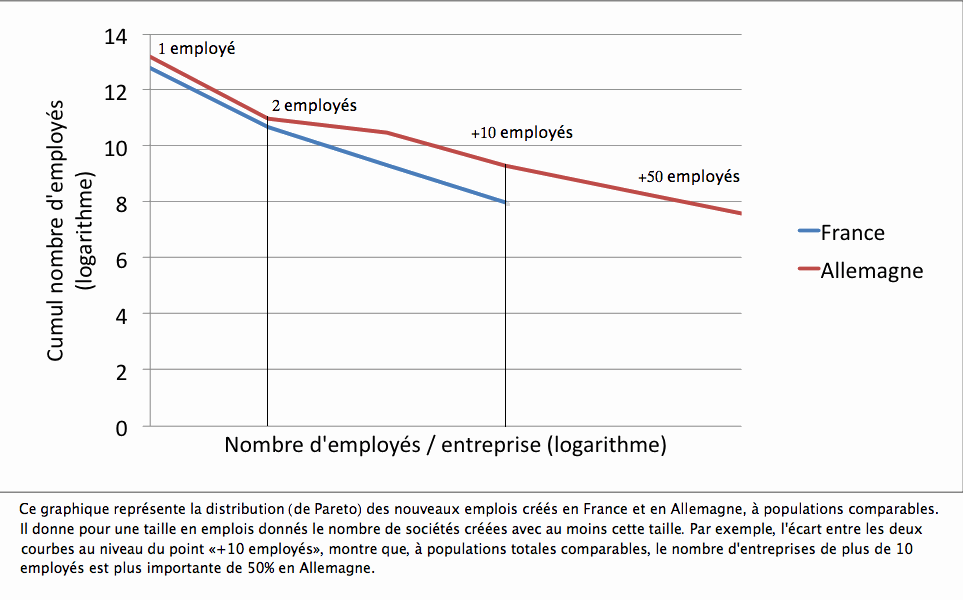
On voit que le logarithme du nombre cumulé d’entreprises à partir des plus grosses est une fonction linéaire du logarithme de la taille, sauf pour les premières où le nombre d’entreprises créées avec 1 salarié est plus faible que ne le voudrait la loi et le nombre avec zéro salarié plus élevé.