Il est possible que les taux de transfert dans une population d’entreprises soient markoviens. Un exemple.
Chaînes de Markov et matrices de transfert.
Un champ de la DEME (Démographie des entreprises) qui reste à explorer sur le plan théorique est celui permettant de décrire une population (celles des entreprises ou des emplois de ces entreprises ou de leurs capitaux propres) comme des ensembles qui se transforment les uns dans les autres suivant un processus markovien.
On rappelle qu’un processus de Markov est un processus qui lie deux états suivant une probabilité de transfert qui est indépendante des conditions passées.
On peut en effet se demander si l’évolution des classes d’entreprise n’est pas markovien.
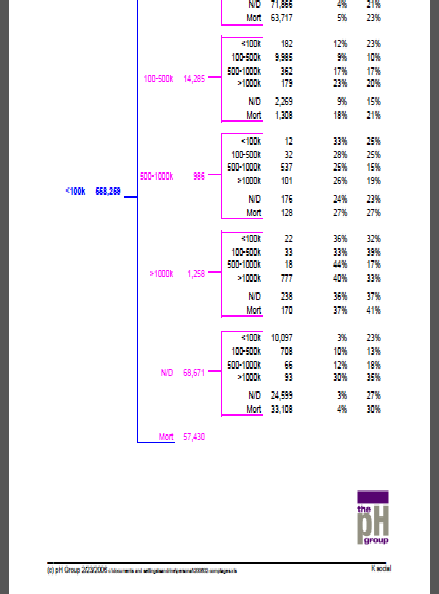
On considère dans le document annexé le nombre d’entreprises dont le capital social au cours d’une période franchit la barrière des 100.000 €.
Dans la période 1997 à 2000, ce sont 16.529 soit 2,96% des 558.259 entreprises dont le capital social en 1997 est inférieur à 100.000 € ; et dans la période 2000 à 2004, 12.313 soit 2,96% des 415.623 entreprises nées avant 1997 qui subsistaient encore en 2000.
Il peut se trouver que cette coïncidence soit un hasard statistique mais une investigation plus approfondie démontrerait peut-être que le pourcentage des entreprises qui franchissent la barrière de capital social de 100.000 € est pour une cohorte (entreprises nées la même année) une constante indépendante du nombre d’années d’existence.
Si c’était bien le cas, la description et le calcul d’une population finale stationnaire d’entreprises, addition de cohortes, deviendrait l’addition de variables exponentielles ce que l’on sait faire facilement et le résultat final qui permettrait de comparer deux économies ne reposerait plus que dans la valeur de l’exposant, comme pour les lois de Pareto.